树和数据库索引

二叉查找树是一棵具有特殊属性的二叉树，每个节点中的关键字必须是:

• 大于左侧子树中存储的所有键
• 小于存储在右侧子树中的所有键

让我们看看它在视觉上意味着什么

这个想法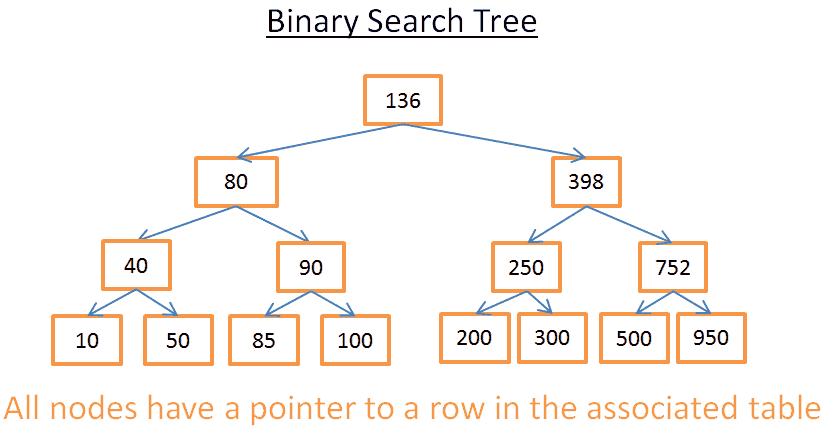

这棵树有N=15个元素。假设我在找208:

• 我从键为136的根开始。因为136<208，所以我查看节点136的右子树。
• 398>208因此，我查看节点398的左侧子树
• 250>208因此，我查看节点250的左侧子树
• 200<208所以，我看节点200的右子树。但是200没有右子树，

  该值不存在

  (因为如果它确实存在，它应该在200的右子树中)

现在假设我要找40

• 我从键为136的根开始。因为136>40，所以我查看节点136的左侧子树。
• 80>40因此，我查看节点80的左侧子树

• 40= 40, 该节点存在

  。我提取了节点中的行的id(图中没有),并在表中查找给定的行id。
• 知道行id让我知道数据在表上的确切位置，因此我可以立即得到它。

最后，这两个搜索都消耗了我在树中的层数。如果你仔细阅读合并排序的部分，你应该看到有log(N)级。所以搜索的代价是log(N)，还不错！

回到我们的问题

但是这个东西非常抽象，所以让我们回到我们的问题。不要用一个愚蠢的整数，想象一下代表上表中某个人的国家的字符串。假设您有一个包含表中“country”列的树:

• 如果你想知道谁在英国工作
• 您查看树以获得代表英国的节点
• 在“英国节点”中，您可以找到英国工人所在行的位置。

如果直接使用数组，这种搜索只需要记录(N)次操作，而不是N次操作。你刚才想象的是一个数据库索引.

您可以为任何列组(一个字符串、一个整数、两个字符串、一个整数和一个字符串、一个日期……)构建一个树索引，只要您有一个比较键(即列组)的函数，这样您就可以建立一个命令 在钥匙中(对于数据库中的任何基本类型都是如此)。

b+树索引

虽然这个树可以很好地获得一个特定的值，但是当你需要的时候，会有一个大问题获取多个元素 两种价值观之间。它的代价是O(N ),因为你必须查看树中的每个节点，并检查它是否在这两个值之间(例如，有序遍历树)。此外，这个操作不是磁盘I/O友好的，因为您必须读取整个树。我们需要找到一种有效的方法范围查询。为了回答这个问题，现代数据库使用以前的树的修改版本，称为B+树。在b+树中:

• 只有最低的节点(叶子)

  储存信息

  (相关表中行的位置)
• 其他节点就在这里

  要路由

  向右节点

  在搜索过程中.

如您所见，有更多的节点(两倍多)。实际上，您有额外的节点，即“决策节点”，它将帮助您找到正确的节点(存储相关表中行的位置)。但是搜索复杂度还是在O(log(N))(只是多了一层)。最大的不同是最低的节点链接到它们的后继节点.

有了这个b+树，如果你在寻找40到100之间的值:

• 你只需要寻找40(或者40之后最接近的值，如果40不存在的话)就像你对之前的树所做的那样。
• 然后使用到后继者的直接链接收集40的后继者，直到你达到100。

假设你找到了M个后继者，树有N个节点。像前面的树一样，搜索特定的节点需要花费log(N)。但是，一旦有了这个节点，就可以在M个操作中获得M个后续节点，并链接到它们的后续节点。这个搜索只需要花费M + log(N)前一个树的操作与N个操作。而且，你不需要读取完整的树(只需要M + log(N)个节点)，这意味着更少的磁盘使用。如果M很小(比如200行)而N很大(1 000 000行),情况就大不一样了。

但是又有新的问题(又来了！).如果在数据库中添加或删除一行(因此在关联的B+树索引中):

• 你必须保持B+树中节点之间的顺序，否则你将无法在混乱中找到节点。
• 你必须在B+树中保持尽可能低的级别数，否则O(log(N))中的时间复杂度将变成O(N)。

换句话说，B+树需要自我排序和自我平衡。幸运的是，通过智能删除和插入操作，这是可能的。但这是有代价的:B+树中的插入和删除都是O(log(N))。这就是为什么你们中的一些人听说过使用太多的索引不是一个好主意。的确，您降低了快速插入/更新/删除行的速度因为数据库需要更新表的索引，每个索引的O(log(N))操作开销很大。此外，添加索引意味着事务管理程序(文末会看到这位经理)。

更多的细节，你可以看看维基百科关于B+树的文章。如果您想要一个数据库中B+树实现的例子，请看这篇文章和这篇文章来自MySQL的一个核心开发者。他们都专注于innoDB(MySQL的引擎)如何处理索引。

注意:一位读者告诉我，由于低级优化，B+树需要完全平衡。

哈希表

我们最后一个重要的数据结构是哈希表。当你想快速寻找值时，它非常有用。此外，理解哈希表将有助于我们稍后理解一种常见的数据库连接操作，称为散列连接。这个数据结构也被数据库用来存储一些内部的东西(比如锁定表或者缓冲池，我们将在后面看到这两个概念)

哈希表是一种数据结构，可以快速找到带有键的元素。要构建哈希表，您需要定义:

• 一把钥匙

  为了你的元素

• 散列函数

  为了钥匙。键的计算散列给出了元素的位置(称为

  大量).

• 比较密钥的函数

  。一旦你找到了正确的桶，你必须使用这个比较在桶中找到你要找的元素。

简单的例子

让我们来看一个直观的例子: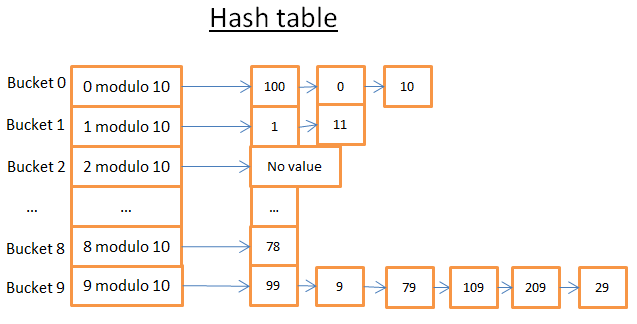

这个散列表有10个桶。因为我很懒，我只画了5个桶，但我知道你很聪明，所以我让你想象另外5个。我使用的哈希函数是密钥的模10。换句话说，我只保留一个元素的键的最后一位数字，以找到它的桶:

• 如果最后一个数字是0，则该元素在桶0中结束，
• 如果最后一个数字是1，则该元素在桶1中结束，
• 如果最后一个数字是2，则该元素在桶2中结束，

• …

我使用的比较函数就是两个整数之间的等式。

假设你想得到78号元素:

• 哈希表计算78的哈希码，即8。
• 它在桶8中查找，找到的第一个元素是78。
• 它还给你78号元素

• 这 搜索只需要2次操作

  (1个用于计算哈希值，另一个用于查找桶内的元素)。

现在，假设你想得到元素59:

• 哈希表计算59的哈希码，即9。
• 它在桶9中查找，找到的第一个元素是99。从99年开始！=59，元素99不是正确的元素。
• 使用相同的逻辑，它查看第二个元素(9)，第三个元素(79)，…，最后一个元素(29)。
• 该元素不存在。

• 搜索需要7次操作.

一个很好的散列函数

如你所见，根据你寻找的价值，成本是不一样的！

如果我现在用关键字的模1 000 000改变散列函数(即取最后6个数字)，第二次搜索只花费1次运算，因为桶000059中没有元素。真正的挑战是找到一个好的散列函数来创建包含非常少量元素的桶.

在我的例子中，找到一个好的散列函数很容易。但这是一个简单的例子，当关键是:

• 字符串(例如一个人的姓)
• 2个字符串(例如一个人的姓和名)
• 2个字符串和一个日期(例如一个人的姓、名和出生日期)

• …

有了好的散列函数， 哈希表中的搜索是O(1).

数组与哈希表

为什么不使用数组呢？

哼，你问了个好问题。

• 哈希表可以是

  一半加载到内存中

  其他存储桶可以留在磁盘上。
• 对于数组，你必须使用内存中连续的空间。如果你要装载一张大桌子

  很难有足够的连续空间.

• 使用哈希表，您可以

  选择您想要的密钥

  (例如一个人的国家和姓氏)。

要了解更多信息，您可以阅读我在Java散列表这是一种有效的哈希表实现；您不需要理解Java就能理解本文中的概念。

本文由本站原创或投稿者首发,转载请注明来源！

本文链接：http://www.ziti66.com/net/html/163.html